Rotacion

La velocidad angular de rotación está relacionada con el momento angular. Para producir una variación en el momento angular es necesario actuar sobre el sistema con fuerzas que ejerzan un momento de fuerza. La relación entre el momento de las fuerzas que actúan sobre el sólido y la aceleración angular se conoce como momento de inercia (I) y representa la inercia o resistencia del sólido a alterar su movimiento de rotación.
Para analizar el comportamiento cinemático de un sólido rígido debemos partir de la idea de que un ángulo θ define la posición instantánea de cualquier partícula contenida en el sólido rígido (CR); este ángulo se mide desde un plano perpendicular al eje de rotación del CR.
Si la posición queda completamente definida por la coordenada angular θ, entonces la velocidad del CR se podrá expresar como:

Mientras que la aceleración quedaría definida por:

La energía cinética de rotación se escribe:

siendo la matriz de inercia.
La expresión del teorema del trabajo en movimientos de rotación se puede expresar así:

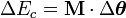
de modo que, la variación de la energía cinética del sólido rígido es igual al producto escalar del momento de las fuerzas por el vector representativo del ángulo girado (Δθ).